 Download Beispiel Regenbogen
Download Beispiel RegenbogenHexaederprinzip am Beispiel eines Rundbogens
 Download Beispiel Regenbogen
Download Beispiel Regenbogen
Auf dieser Seite soll für den 3D-Editor von WinTrack der Befehl [hexaeder] näher betrachtet werden. Hexaeder bedeutet Sechsflächner, er besitzt also 6 Seiten, genau wie ein Würfel und wie ein Quader. Nur ist ein Hexaeder ein viel allgemeineres Gebilde, d. h. seine Seiten können alle verschieden groß sein und brauchen auch nicht parallel zueinander sein. Um nicht nur Theorie zu haben, wählen wir zur Veranschaulichung gleich ein praktisches Beispiel wo wir den Hexaederbefehl geradezu anwenden müssen. Da der 3D-Editor keinen Befehl für Rundbögen bereitstellt, müssen wir Bögen also mittels mehr oder weniger vielen Hexaedern näherungsweise nachbilden. Es wäre ungeschickt einen Rundbogen gleich irgendwie im freien Raum hinein konstruieren zu wollen. Viel geschickter, wir wählen uns dazu erst einmal eine ebene, zweidimensionale Fläche aus; sagen wir die x/z-Ebene des 3D-Editors. Für unseren Rundbogen nehmen wir einen Halbkreis K1 mit Durchmesser d1=20 LE (LE = LängenEinheit; im Listing von TEdit3D wählen wir z. B. einen Faktor von 10, dann sind dort 20 LE = 200mm). Der Bogen soll eine Stärke von 1 LE haben, somit nehmen wir einen zweiten Halbkreis K2 mit Durchmesse d2=18 LE. Dies können wir z.B. auf Millimeterpapier zeichnen ( 1:1, oder besser noch in einem vergrößerten Maßstab, um die Koordinaten darin genauer ablesen zu können, z. B. 2:1 oder 4:1). Wir erhalten also folgende Zeichnung:
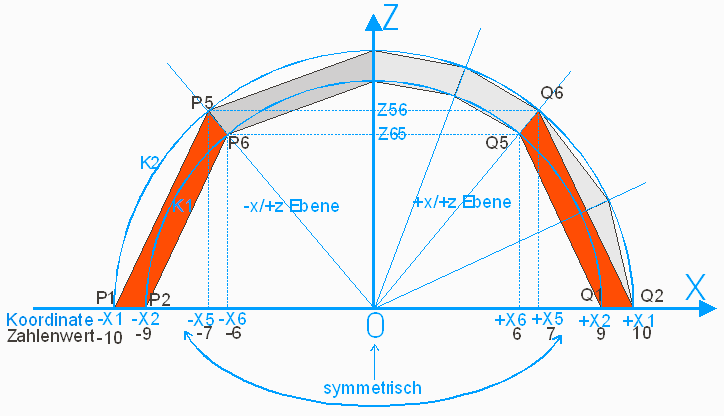
Der exakte Rundbogen wird durch die beiden blauen Halbkreise K1 und K2 dargestellt, die in der x/z-Ebene liegen. Wir teilen den linken Viertelkreis in der Mitte auf: Punkt P5 und P6. Damit erhalten wir unseren ersten rot dargestellten Hexaeder in einer seitlichen Ansicht mit den Punkten P1,P2,P6,P5. Haben wir unseren Rundbogen auf Millimeterpapier gezeichnet, können wir die ersten x-Koordinaten dort ablesen oder ausrechnen: P1= -10, P2= -9, P5= -7.07, P6= -6.36. Da wir geschickter Weise unseren Halbkreisbogen symmetrisch zum Koordinatenursprung gelegt haben, sehen wir, dass der rechte Bogen symmetrisch zum linken ist. Damit stehen uns auch die x- Koordinaten des rechten Hexaeders schnell zur Verfügung: Q1= +9, Q2= +10, Q5= +6.36, Q6= +7.07. Die z-Koordinaten für P1, P2, Q1, und Q2 sind jeweils 0; die z-Koordinaten von P6 und Q5 sind 6.36, die von P5 und Q6 sind 7.07. Zu den y-Koordinaten kommen wir später, wir betrachten momentan nur die 2-dimensionale x/z-Ebene! Wir erkenn, dass unser Bogen noch ziemlich eckig ist. Eine nochmalige Unterteilung (rechtes Kreisviertel, hell grau eingezeichnet) würde sich dem Bogen bereits besser anpassen. Aber uns geht es hier erst einmal um das Prinzip Hexaeder und wir bleiben bei der groben Darstellung und wenden uns den letzten noch fehlenden y-Koordinaten zu:
 Download Beispiel
Hexaederprinzip
Download Beispiel
Hexaederprinzip
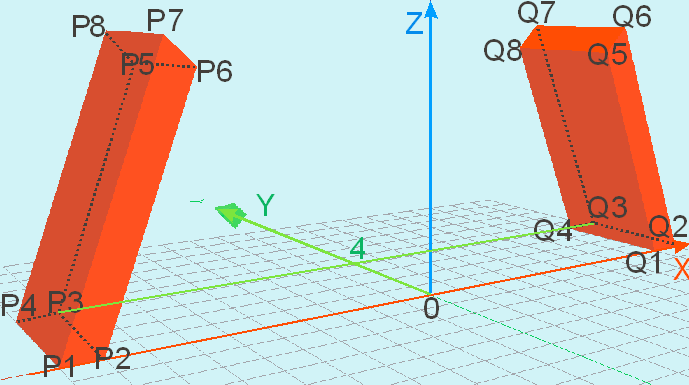
Wir weisen unserem Rundbogen noch Breite von 4 LE zu und erkenn, dass die Punkte P1, P2, P5 und P6 alle eine y-Koordinaten von 0 haben; die Punkte P3, P4, P7 und P8 alle eine y-Koordinate von 4 haben (das gleiche gilt auch für die Q-Punkte). Acht geben müssen wir jetzt nur noch auf die Reihenfolge der Punkte in der wir diese in den Hexaederbefehl eingeben, denn sonst stimmen später die Farben nicht! Der Befehl in TEdit3D lautet:
// hexaeder: Körper mit 6 ebenen Flächen
// definiert durch 8 Punkte im Raum, deren Reihenfolge wichtig ist. (sonst stimmen die Farben nicht !)
// Punkte 1-4: unten: beginnend mit links vorne, rechts vorne, rechts hinten, links hinten,
// Punkte 5-8: oben: beginnend mit links vorne, rechts vorne, rechts hinten, links hinten,
also: P1, P2, P3,P4, P5, P6, P7, P8, und Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8 damit erhalten wir:

Da Hexaederkoordinaten (Punkte) des linken Viertelkreises spiegelsymmetrisch zu denen des rechten Viertelkreises sind, lässt sich folgender Zusammenhang erkennen:

Man braucht sich also lediglich die Koordinaten der Hexaeder im linken Viertelkreis zu verschaffen, dann entsprechende Vorzeichen einfach umzukehren, und die Punkte kreuzweise vertauschen, um die Hexaeder in richtiger Reihenfolge für die rechte Seite zu bekommen. Die eckigen Pfeilklammern kennzeichnen Punkte mit gleichen x/z-Koordinaten, die sich nur in der y-Koordinate unterscheiden. Dieses Wissen kann man dazu verwenden um (a) richtige Reihenfolge der Punkte, (b) schnelles Erstellen der rechten Hexaeder durch Kopieren, Vorzeichenwechsel und Vertauschen der Koordinaten von linken Hexaedern, (c) schnelle Überprüfung auf Fehler zu erreichen. Diese Arbeit wird leichter, wenn man im Listing zwischen den einzelnen Punkten entsprechende Leerzeichen einfügt, damit die Darstellung übersichtlich wird.
Solange man mit dem Hexaederbefehl, insbesondere bei der Erstellung von Bögen, noch nicht so geübt ist, kann auch eine Tabelle hilfreich sein, in der man alle Koordinaten erst einmal einträgt:
 Download Hexaeder_Formblatt
Download Hexaeder_Formblatt
Hier ein Beispiel eines Torbogens auf Millimeterpapier
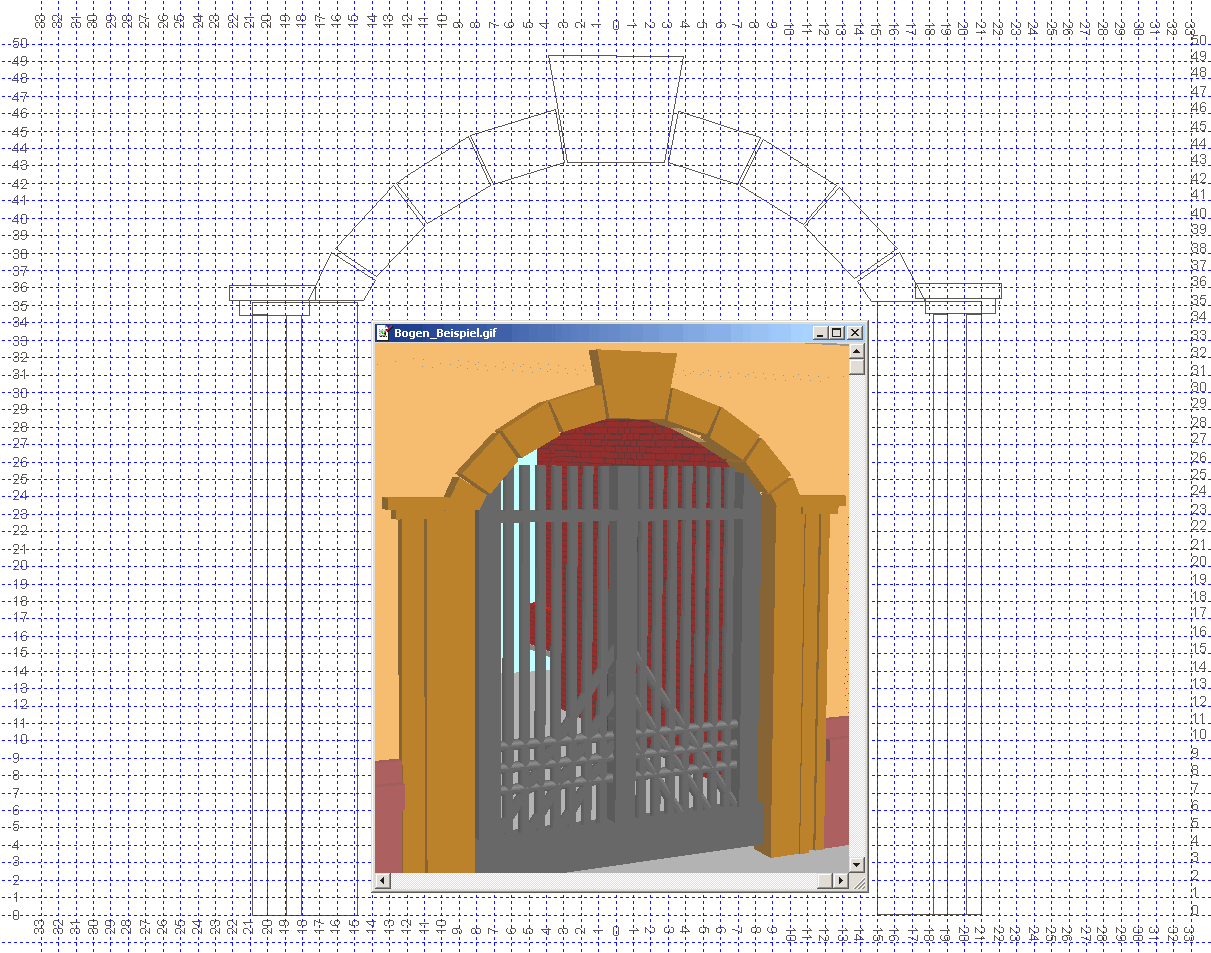 :
:
Anmerkungen:
Man kann auch Originalmodelle scannen und in ein Zeichenprogramm importieren (z.B. CorelDraw), ein Hilfslinienraster (Millimeterpapier) anlegen, alles vergrößern, Linien nachzeichnen, etc. und Koordinaten dort ablesen.
Es gibt auch kleine Programme mit denen man die Koordinaten von verschiedenen geometrischen Körpern berechnen kann. Ein solches ist z. B. Geometrix. (das oberste Beispiel "Regenbogen" wurde damit berechnet). Hier der Link zu Geometrix.
Ein Download-Beispiel Torbogen indem Geometrix zur Berechnung in TEdit3D herangezogen wurde.